机器学习算法（一）—— KNN

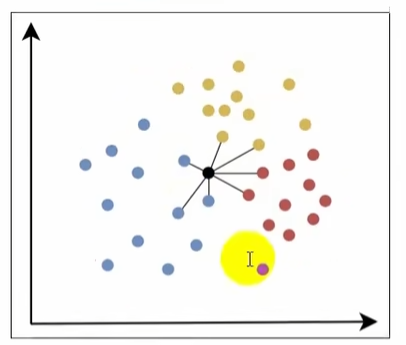
1 KNN算法（k-近邻算法 K-Nearest Neighbors）

是一种基本的分类与回归算法，属于监督学习算法

1.1 工作原理

  • 计算距离；计算待分类样本跟训练集中每个样本的距离。
  • 选择K个近邻：根据计算的距离，选择距离最近的k个样本。
  • 投票或平均：
    • 分类任务：统计K个近邻各类别的数量，将待分类样本归为数量最多的类别。
    • 回归任务：取K个近邻的平均值作为预测结果。

1.2 关键参数

  • 距离度量方法
  • K值：K小容易过拟合（容易模拟噪声），K大容易欠拟合（如将K = n，只用计算哪一类最多）

1.3 优缺点：

  • 优点：
    • 简单直观，易于理解和实现
    • 无需训练过程，直接利用训练数据进行预测
  • 缺点：
    • 计算量大，尤其是训练集较大时。
    • 对噪声数据较敏感。

1.4 使用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
# 分类
from nltk.app.nemo_app import colors
from sklearn.neighbors import KNeighborsClassifier
import numpy as np
import matplotlib.pyplot as plt
# 准备数据
X = np.array([[2, 1],[3, 1],[1, 4],[2, 6]])
y = np.array([0, 1, 0, 1])
# 定义KNN分类模型
knn = KNeighborsClassifier(n_neighbors=2, weights='distance')
# 模型训练
knn.fit(X, y)
# 预测
x = np.array([[4, 9]])
x_class = knn.predict(x)
print(x_class)
# 画图
fig, ax = plt.subplots()
ax.axis("equal")
# 使用布尔索引将两类点分开
X1 = X[y == 0]
X2 = X[y == 1]
# 定义不同的颜色画两组点
colors = ["C0", "C1"]
plt.scatter(X1[:, 0], X1[:, 1], c = colors[0])
plt.scatter(X2[:, 0], X2[:, 1], c = colors[1])
# 新点的颜色
x_color = colors[0] if x_class == 0 else colors[1]
plt.scatter(x[:, 0], x[:, 1], c = x_color)
plt.show()
---------------------------------------------------------------------------------------
# 回归
from sklearn.neighbors import KNeighborsRegressor
# 准备数据
X = [[2, 1],[3, 1],[1, 4],[2, 6]]
y = [0, 1, 0, 1]
# knn回归模型
knn = KNeighborsRegressor(n_neighbors=2)
knn.fit(X, y)
# 预测
x = [[4, 9]]
x_class = knn.predict(x)
print(x_class)

答案：1)下图；2）0.5

2 常见距离度量方式（了解）

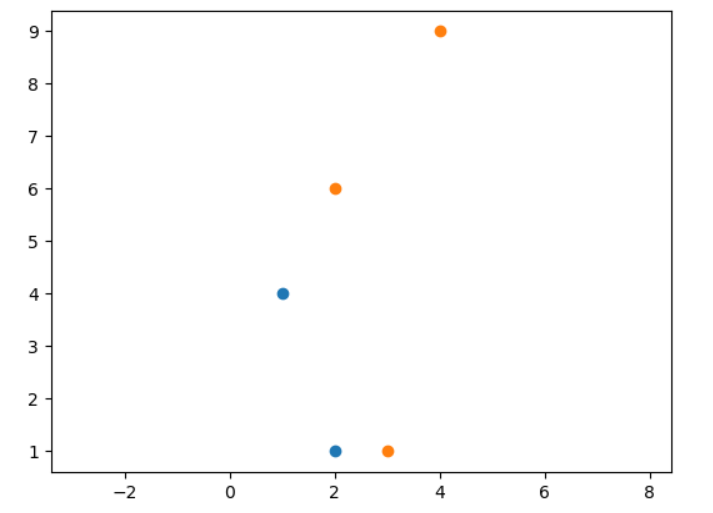
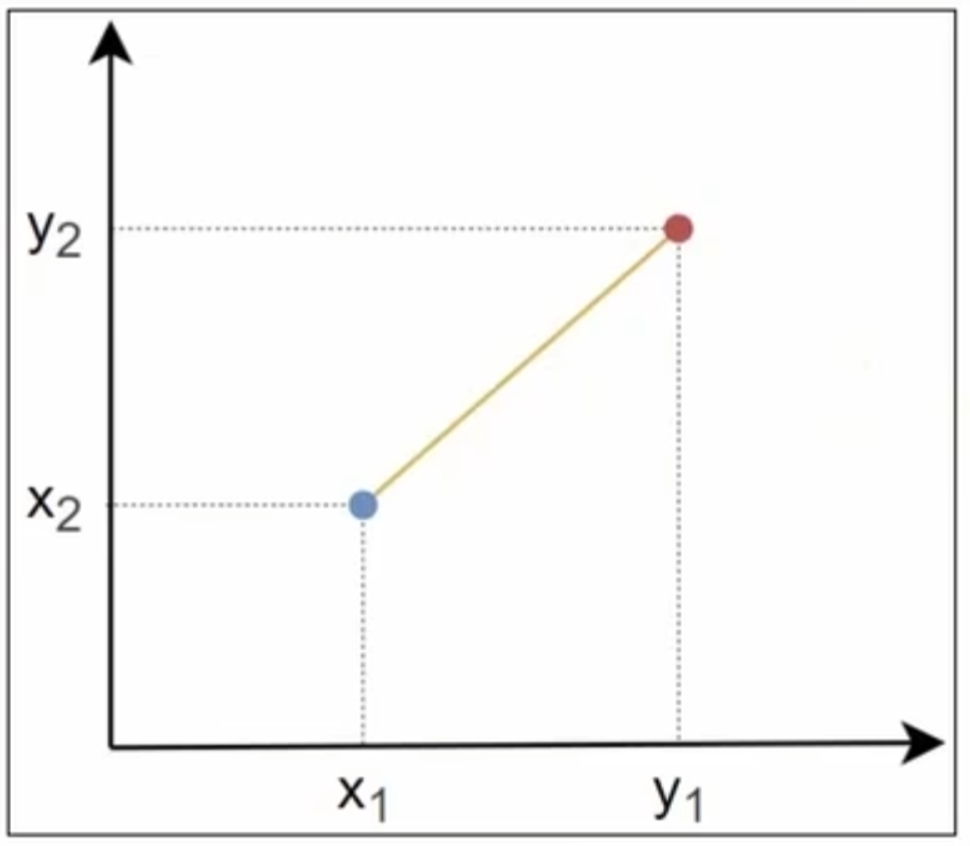
2.1 欧氏距离

  • 欧几里得距离指连接两点的线段的长度
  • 点 和 之间的欧氏距离

image-20251027213826400

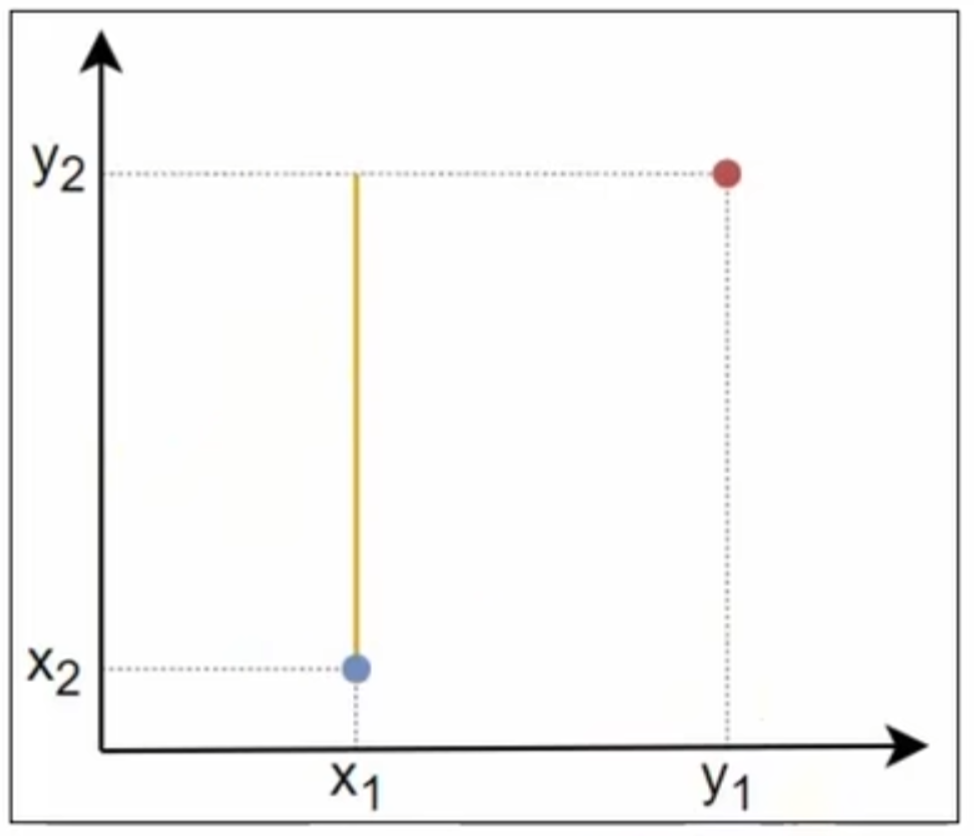
2.2 曼哈顿距离

  • 曼哈顿距离是两点在标准坐标系上的绝对轴距之和
  • 点 和 之间的曼哈顿距离

img

2.3 切比雪夫距离

  • 切比雪夫距离是两点各坐标数值差的最大值
  • 点 和 之间的切比雪夫距离 （）

image-20251027213903195

2.4 闵可夫斯基距离

  • 闵可夫斯基距离是一种用于度量多维空间中两点间距离的通用方法，点 ） 和 之间的闵可夫斯基距离 。p越小，对多个维度的差异更敏感；p越大，更关注最大维度的差异。
  • 通过调整参数p，闵可夫斯基距离可以退化为以下经典距离：
    • 曼哈顿距离：p = 1，
    • 欧氏距离：p = 2，
    • 切比雪夫距离：p = ∞，（）

3 归一化与标准化

3.1 归一化

3.1.1 定义

  • 将数据按比例缩放到一个固定范围 (通常是[0,1]或[1,-1])。
  • ，[0,1]
  • ，[1,-1]

3.1.2 目的

  • 消除量纲差异：不同特征的单位或量纲可能差异巨大化，归一化可消除这种差异，避免模型被大范围特征主导
  • 加速模型收敛：对于梯度下降等优化算法，归一化后特征处于相近的尺度，优化路径更平滑，收敛速度更快。
  • 适配特定模型需求：某些模型（如神经网络、K近邻、SVM）对输入数据的范围敏感，归一化能显著提升其性能。
  • 使用场景
    • 归一化不改变原始分布形状，但对异常值比较敏感。当数据分布有明显边界（如图像像素值、文本词频），或模型对输入范围敏感时可以优先考虑归一化。

3.1.3 API使用

1
2
3
4
5
6
7
8
9
10
11
12
from sklearn.preprocessing import MinMaxScaler
X = [[2, 1],[3, 1],[1, 4],[2, 6]]
# 定义归一化类的参数
scaler = MinMaxScaler(feature_range=(-1, 1))
# 将缩放器应用到特征上
X_scaler = scaler.fit_transform(X)
print(X_scaler)
# 结果：
[[ 0.  -1. ]
 [ 1.  -1. ]
 [-1.   0.2]
 [ 0.   1. ]]

3.2 标准化

3.2.1 定义

  • 将数据调整为均值为0、标准差为1的标准分布 ，其中 是平均值， 是标准差。

3.2.2 目的

  • 适应数据分布：将数据转化为均值为0、标准差为1的分布，适合假设数据服从正态分布的模型（如线性回归、逻辑回归）。
  • 稳定模型训练：标准化后的数据对异常值的敏感度较低（相比归一性），鲁棒性更强。
    • 注：鲁棒性指系统在出现异常、危险情况下能够保持健壮和强壮的特性。比如，计算机软件在出现错误、故障或攻击时不崩溃或死机就是具有鲁棒性。鲁棒性可以分为稳定鲁棒性和性能鲁棒性。
  • 统一特征尺度：与归一化类似，标准化也能消除量纲差异，但更关注数据的统计分布而非固定范围。

3.2.3 使用场景

  • 大多数场景下标准化更通用，尤其是数据分布未知或存在轻微异常值时。

3.2.4 API使用

1
2
3
4
5
6
7
8
9
10
from sklearn.preprocessing import StandardScaler
X = [[2, 1],[3, 1],[1, 4],[2, 6]]
scaler = StandardScaler()
X_scaler = scaler.fit_transform(X)
print(X_scaler)
# 输出
[[ 0.         -0.94280904]
 [ 1.41421356 -0.94280904]
 [-1.41421356  0.47140452]
 [ 0.          1.41421356]]

4 案例：心脏病预测

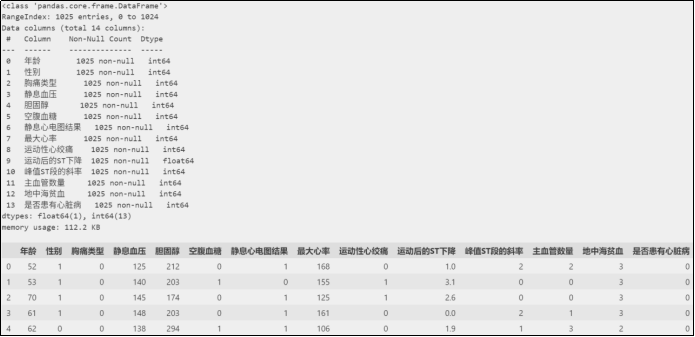
4.1 数据集说明

Heart Disease数据集

  • 年龄：连续值
  • 性别：0-女，1-男
  • 胸痛类型：0-典型心绞痛，1-非典型心绞痛，2-非心绞痛，3-无症状
  • 静息血压：连续值，单位mmHg
  • 胆固醇：连续值，单位mg/dl
  • 空腹血糖：1-大于120mg/dl，0-小于等于120mg/dl
  • 静息心电图结果：0-正常，1-ST-T异常，2-可能左心室肥大
  • 最大心率：连续值
  • 运动性心绞痛：1-有，0-无
  • 运动后的ST下降：连续值
  • 峰值ST段的斜率：0-向上，1-水平，2-向下
  • 主血管数量：0到3
  • 地中海贫血：一种先天性贫血，0-正常，1-固定缺陷，2-可逆缺陷
  • 是否患有心脏病：标签，0-否，1-是

4.2 加载数据集

1
2
3
4
5
6
7
8
import pandas as pd

# 加载数据集
heart_disease = pd.read_csv("data/heart_disease.csv")
# 处理缺失值
heart_disease.dropna()
heart_disease.info()
heart_disease.head()

4.3 数据集划分

1
2
3
4
5
6
7
from sklearn.model_selection import train_test_split

# 划分特征和标签
X = heart_disease.drop("是否患有心脏病", axis=1)  # 特征
y = heart_disease["是否患有心脏病"]  # 标签
# 将数据集按7:3划分为训练数据与测试数据
x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=100)

4.4特征工程

4.4.1 特征转换

数据集中包含多种类型的特征：

  • 类别型特征（需要特殊处理）
    • 胸痛类型：4种分类（名义变量）
    • 静息心电图结果：3种分类（名义变量）
    • 峰值ST段的斜率：3种分类（有序变量）
    • 地中海贫血：4种分类（名义变量）
  • 数值型特征（可直接标准化）：年龄、静息血压、胆固醇、最大心率、运动后的ST下降、主血管数量
  • 二元特征（保持原样）：性别、空腹血糖、运动性心绞痛

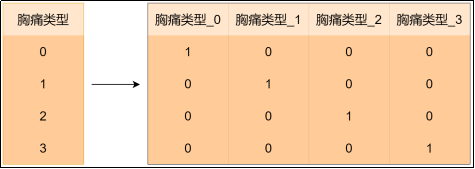
对于类别型特征，直接使用整数编码的类别特征会被算法视为有序数值，导致错误的距离计算（例如：会认为 胸痛类型=1 和 胸痛类型=2 之间的差异比 胸痛类型=1和 胸痛类型=3之间差异更小，而实际上它们都是类别）。使用 独热编码（One-Hot Encoding）可将类别特征转换为二元向量，消除虚假的顺序关系。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
from sklearn.preprocessing import StandardScaler, OneHotEncoder
from sklearn.compose import ColumnTransformer

# 数值型特征
numerical_features = ["年龄", "静息血压", "胆固醇", "最大心率", "运动后的ST下降", "主血管数量"]
# 类别型特征
categorical_features = ["胸痛类型", "静息心电图结果", "峰值ST段的斜率", "地中海贫血"]
# 二元特征
binary_features = ["性别", "空腹血糖", "运动性心绞痛"]
# 创建列转换器
preprocessor = ColumnTransformer(
    transformers=[
        # 对数值型特征进行标准化
        ("num", StandardScaler(), numerical_features),
        # 对类别型特征进行独热编码，使用drop="first"避免多重共线性
        ("cat", OneHotEncoder(drop="first"), categorical_features),
        # 二元特征不进行处理
        ("binary", "passthrough", binary_features),
    ]
)
# 执行特征转换
x_train = preprocessor.fit_transform(x_train)  # 计算训练集的统计信息并进行转换
x_test = preprocessor.transform(x_test)  # 使用训练集计算的信息对测试集进行转换

4.4.2 避免多重共线性

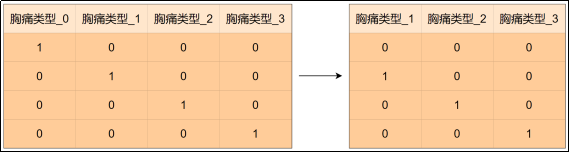
  • drop=“first“是独热编码中的一个参数，它的核心目的是避免多重共线性（Multicollinearity）。

  • 多重共线性是指特征之间存在高度线性相关关系的现象。例如特征胸痛类型包含4个类别（0、1、2、3），若直接进行独热编码会生成4个新列（胸痛类型_0、胸痛类型_1、胸痛类型_2、胸痛类型_3），此时这4列满足

    • 胸痛类型_0+胸痛类型_1+胸痛类型_2+胸痛类型_3=1

  • 这种完全线性相关关系会导致特征矩阵的列之间存在完美共线性。

  • 当特征矩阵存在多重共线性时，模型参数估计会变得不稳定（矩阵不可逆或接近奇异），导致系数估计值方差增大、模型可解释性下降、过拟合等问题。

  • 在独热编码时设置drop=“first”，会删除每个类别特征的第1列，从而打破完全共线性。比如特征胸痛类型会生成3列（胸痛类型_1、胸痛类型_2、胸痛类型_3），此时 胸痛类型_1=0，胸痛类型_2=0，胸痛类型_3=0 隐含代表 胸痛类型_0=1

虽然KNN不直接受多重共线性影响（不像线性模型），但使用drop=“first“也能够减少冗余特征，提升计算效率。

4.5 模型训练与评估

1
2
3
4
5
6
7
8
from sklearn.neighbors import KNeighborsClassifier

# 使用K近邻分类模型，K=3
knn = KNeighborsClassifier(n_neighbors=3)
# 模型训练
knn.fit(x_train, y_train)
# 模型评估，计算准确率
knn.score(x_test, y_test)

4.6 模型的保存

可以使用Python的joblib库保存训练好的模型：

1
2
3
import joblib

joblib.dump(knn, "knn_heart_disease")

加载先前保存的模型：

1
2
3
4
5
6
# 加载模型
knn_loaded = joblib.load("knn_heart_disease")
# 预测
y_pred = knn_loaded.predict(x_test[10:11])
# 打印真实值与预测值
print(y_test.iloc[10], y_pred)

5 模型评估与超参数调优

5.1 网格搜索

  • 网格搜索（Grid Search）是一种系统化的超参数调优方法，通过遍历预定义的超参数组合，找到使模型性能最优的参数配置。通过自动化调参避免手动试错，提高效率。
  • 网格搜索通常嵌套交叉验证，与交叉验证结合以提高调参的可靠性：
    • 外层循环：遍历参数网格中的每个参数组合。
    • 内层循环：对每个参数组合使用交叉验证评估模型性能。

5.2 对心脏病预测模型进行超参数调优

对模型训练与评估部分进行修改，使用sklearn.model_selection.GridSearchCV进行交叉验证和网格搜索：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import GridSearchCV

knn = KNeighborsClassifier()
# 网格搜索参数，K值设置为1到10
param_grid = {"n_neighbors": list(range(1, 10))}
# GridSearchCV(estimator=模型, param_grid=网格搜索参数, cv=k折交叉验证)
knn = GridSearchCV(estimator=knn, param_grid=param_grid, cv=10)

# 模型训练
knn.fit(x_train, y_train)
print(pd.DataFrame(knn.cv_results_))  # 所有交叉验证结果
print(knn.best_estimator_)  # 最佳模型
print(knn.best_score_)  # 最佳得分

# 使用最佳模型进行评估
knn = knn.best_estimator_
print(knn.score(x_test, y_test))